機械学習モデルの予測結果を説明するための力が欲しいか...？

はじめに

最近はAIや機械学習などの単語がビジネスで流行っていて、世はAI時代を迎えている。QiitaやTwitterを眺めているとその影響を受けて、世の多くのエンジニアがAIの勉強を始め出しているように見受けられる。

さらに、近年では機械学習のライブラリも充実しており、誰でも機械学習を実装することができる良い時代になってきた。

その一方で、特徴選択を行い精度を向上させたり、機械学習の出した答えがどの特徴に基づいて判断されたのかを理解したりするには、モデルに対する理解やテクニックが必要となる場合も多々ある。複雑なモデルになると人間には解釈が困難で説明が難しい。近頃流行りのDeep Learning系のモデルだと頻繁に「なんかよくわからないけどうまくいきました」となっていると思う。

一般的なエンジニアとしては、この点が割と課題なんじゃないかと勝手に思っている。というか、私が課題に感じている。（特に実業務で機械学習していない上に、エンジニアでもないが）

そんなわけで、今回はこの課題を解決するためのツールであるLIME(Local Interpretable Model-agnostic Explainations)が興味深かったので、紹介していこうかと思う。
※本記事はLIMEのアルゴリズムの説明となるため、LIMEを実際に利用したい方はGitHub - marcotcr/lime: Lime: Explaining the predictions of any machine learning classifierでpythonのライブラリインストール方法とチュートリアルが載っているので、そちらをご参照ください。

モデルの説明とは何か

LIMEの紹介に移る前に機械学習モデルを説明するとはどういうことなのか整理していきたい。
機械学習モデルの説明には下記の説明の2種類が考えられる。

explaining prediction(予測の説明)

データ一つに対する機械学習モデルの分類器による予測結果に対して、どうして分類が行われたのかを説明すること。(下記の図はイメージ)
f:id:gat-chin321:20170107164420p:plain
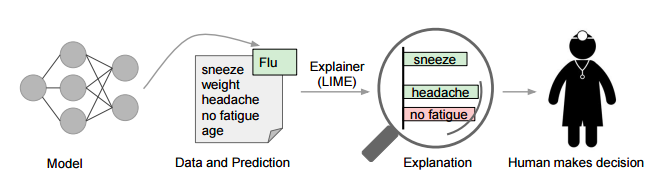
(出典: https://arxiv.org/pdf/1602.04938.pdf)

explaining models(モデルの説明)

分類器がどういう性質を持っているのかを説明すること。

(出典: Introduction to Local Interpretable Model-Agnostic Explanations (LIME) - O'Reilly Media)

LIMEはこのうち、explaining predictionを行うためのアルゴリズムである。
explaining modelsについては、SP-LIMEと呼ばれるアルゴリズムが論文に記載されているので、そちらを参照されたし。(気が向けば、SP-LIMEについても記事を書く)

LIME(Local Interpretable Model-agnostic Explainations)の紹介

LIMEとは？

KDD2016で採択された『“Why Should I Trust You?” Explaining the Predictions of Any Classifier』というタイトルの論文で発表されたアルゴリズム。分類器がどのように判断してラベリングを行なったのかを人間でも解釈できるような形で提示してくれる。
このアルゴリズムはあるデータを分類した結果、それぞれの特徴がどの程度分類に貢献しているかを調べることで分類器の予測結果を説明している。また、分類器の予測結果を用いるため、任意の分類器に適用できる特徴がある。

LIMEのアイデア

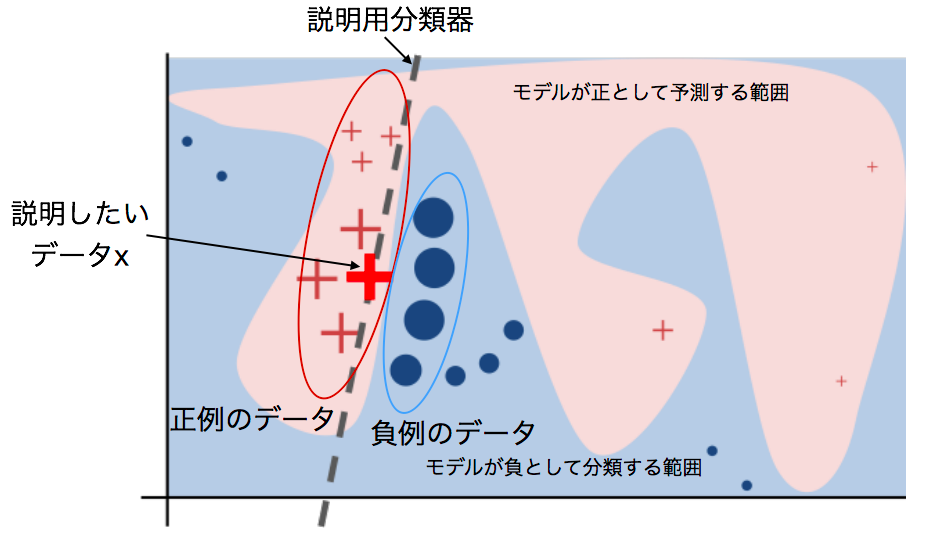
データ $x$ の周辺からサンプリングしたデータを用いて、説明したい分類器の出力と近似するように解釈可能な（かつ単純な）モデルを学習させる。その後、得られた分類器を用いて分類結果の解釈を行う。下記がイメージ図（論文から抜粋した図を編集）。

f:id:gat-chin321:20170106191925p:plain
(出典: https://arxiv.org/pdf/1602.04938.pdf)

説明用分類器の学習方法

説明用分類器 $g$ はデータ $x$ の周辺で $f$ の結果と近似するようにしたい。
そうするために、下記の目的関数を利用して学習する。

${\displaystyle \DeclareMathOperator*{\argmin}{arg\,min} \begin{equation} \xi(x) = \argmin_{g \in G} L(f, g, \pi_x) + \Omega(g) \end{equation} }$

$G$ : 解釈可能なモデルの集合
$g$ : Gのうちの一つのモデル。例えば、線形モデルなど
$f$ : 説明したい分類器
$\pi_x$ : データ $x$ との距離
$L(f, g, \pi_x)$ : データ $x$ の周辺で $f$ と $g$ の結果がどれだけ違っているか（ $L$ は損失関数ともいう）
$\Omega(g)$ : 説明用分類器 $g$ の複雑さ

上記の内容から、 $\xi(x)$ はデータ $x$ の周辺で $f$ と $g$ の結果についての食い違い $L(f, g, \pi_x)$ と説明用分類器 $g$ の複雑さの和を最小にする $g$ の集合を求めるものであると言える。
ここで、 $\Omega(g)$ はテキスト分類の場合、解釈可能なモデルの特徴表現を単語の有無 ${0,1}$ のBag-of-Words法(単語袋詰め)とし、単語の数(次元数)に限度Kを設定することで、説明が解釈可能であることを保証するためのものらしい。
画像データの場合はsuper-pixelsと呼ばれる任意のアルゴリズムを使用して計算されるものを用いて解釈可能なモデルの特徴表現とする。
ここで、この特徴表現は ${0,1}$ の2値で表され、1は元のsuper-pixels、0はグレーアウトされたsuper-pixelsを示す。
ここまでで $\xi(x)$ について、何となくというレベルでは理解ができたと思いたい。
そこで、次は $L(f, g, \pi_x)$ の数式についても見ていこう。

${\displaystyle L(f, g, \pi_x) = \sum_{z,z' \in Z } \pi_x (z) (f(z) - g(z'))^2 }$

$Z$ : $x$ の周辺のデータの集合
$z'$ : 非ゼロ要素を一部だけ含むサンプリングにより生成された2値のスパースな点。

　 $z' \in \{0,1\}^d$ で定義される

$z$ : $z'$ を用いて復元された元のサンプルの特徴表現。 $z \in R^d$ で定義される

この式を見る限り、 $x$ の周辺のデータにおける $\pi_x (z)$ で重み付けした残差平方和を出している。
残差平方和自体は正解データ(今回の場合、説明したい分類モデルの予測結果)と推定モデルの予測結果との間の不一致を評価する尺度なので、わかりやすいかと思う。
また、 $\pi_x (z)$ で重み付けしている理由について理解するため、 $\pi_x (z)$ の式を見ていこう。

${\displaystyle \pi_x (z) = exp\Bigl(\frac{-D(x,z)^2}{\sigma^2}\Bigr) }$

$D(x,z)$ : $x$ と $z$ との距離関数(例えば、テキストならコサイン類似度、画像ならL2ノルムなどを利用する)
$\sigma$ : 指数カーネルのカーネル幅

$\pi_x (z)$ の式はカーネル関数であり、xとzの2変数間の類似度を算出している。 $\pi_x (z)$ はテキトーに0から1までの値を入れて見て計算すればわかると思うが、サンプルが近ければ近いほど値が小さくなる。これで重み付けすることで、 $x$ と $z$ との距離が近いサンプルの場合は損失 $L(f, g, \pi_x)$ が小さくなりやすくなり、逆に距離が遠いサンプルの場合は損失が高くなる。この重み付けのおかげで、ロバストなモデルとなっている。
最後は $\Omega(g)$ について掘り下げていく。 $\Omega(g)$ の式を見ていこう。

${\displaystyle \Omega(g) = \infty \mathbb{1} [||w_g||_0 > K ] }$

$\Omega(g)$ は利用する特徴がたかだか単語数(もしくはsuper-pixels)K程度だけとすることを示しているっぽい。
利用する特徴 $\Omega(g)$ の選択は、方程式 $\xi(x)$ から直接解くことで実現することは難しい。
そのため、まず著者らがK-Lassoと呼んでいる、Lassoで正則化パスを使用して利用する特徴をK個選択し、最小二乗法を介して重みを学習する方法によって、利用する特徴 $\Omega(g)$ の選択についての解と近似させる。
これにより、方程式 $\xi(x)$ を解くことができるようになるため、線形モデル(Githubのコードを読む限りではRidge回帰)で学習を行う。
この学習した線形モデルの偏回帰係数を確認することで、選択された特徴について、どれだけ分類に貢献しているかの説明を行うことができる。

ここまで、説明した内容が下記の図のAlgorithm 1 である。
f:id:gat-chin321:20170107152919p:plain
(出典: https://arxiv.org/pdf/1602.04938.pdf)

Algorithm 1 は個々の予測についての説明を生成するので、その複雑さはデータセットのサイズに依存するのではなく、 $f(x)$ を計算する時間とサンプル数 $N$ に依存するらしい。

検証と考察

検証もどき

今回はマルウェアと正常なプログラムのAPIコールのデータセットが手元にあったので、著者らのLIMEパッケージを使ってみることにした。
データセットは下記からとってきたものだ。
Malicious datasets * - Csmining Group

データセットの内容はファイル形式がcsv、マルウェアの数が320検体、正常なプログラムの数が68検体という微妙な数となっている。

簡単な検証の結果は下記の通りだった。
github.com

検証用にランダムフォレストを使ってマルウェアと正常なプログラムを分類した。
ランダムフォレストを選んだ理由は、直線ではない分離境界を引いてくれてかつ、そのモデル自体が重視している特徴を出せるからだ。他にいい分類器があれば教えていただきたいところ。
脳細胞が死んでいるので、データを学習用(マルウェアが310検体と正常なプログラム68検体)とテスト用(マルウェアが10検体)に手で分けた。
そのテスト用の予測結果はf1_scoreが1.0となった。マルウェアと正常なプログラムのAPIコールを用いた分類は割と線形分離可能なものが多い印象なので、交差検証とかしていない上に、テスト数も少ないのでこんなもんではあるとは思う。

考察もどき

結果の考察だが、LIMEで出力された "GetFileAttributesW"、"GetFullPathNameW"、"GetLongPathNameW"
などの特徴が、ランダムフォレストの特徴ランキングの上位に食い込んでいることがわかる。
LIMEで出力されるのは、そのデータ単体のどの特徴を重視して分類したかであるexplaining predictionsにあたり、ランダムフォレストの特徴ランキングは多分explaining modelsなので、厳密に比較すべきではないかもしれない。
しかし、モデル自体が重視している特徴はexplaining predictionsの上位に来ても直感的にはおかしくないと思うので、いい感じになんか説明できている気がする。

参考文献

LIME論文：

“Why Should I Trust You?” Explaining the Predictions of Any Classifier
https://arxiv.org/pdf/1602.04938.pdf

LIMEコード：

github.com

参考にした資料：

sssslide.com

KDD2016勉強会資料 from Toshihiro Kamishima